Gaussian Process Research
A series of works on scaling and improving Gaussian Process models
This project encompasses a series of works focused on making Gaussian Process models more scalable and practical for real-world applications.
Key Publications
Improving GAN Training via Binarized Representation Entropy (BRE) Regularization
Scaling Gaussian Processes (PhD Thesis)
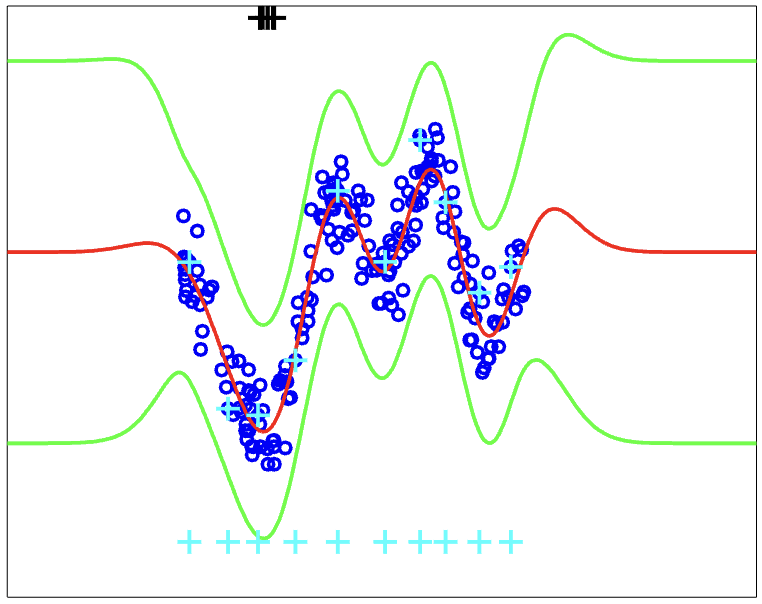
My PhD thesis at University of Toronto focused on developing methods to scale Gaussian Process models to large datasets. The work combines theoretical insights with practical algorithms for making GPs more computationally efficient while maintaining their powerful probabilistic modeling capabilities.
Efficient Optimization for Sparse Gaussian Process Regression
A key contribution was developing an efficient optimization algorithm for selecting inducing points in sparse Gaussian Process regression. The method achieves linear time and space complexity while maintaining state-of-the-art performance.
Generalized Product of Experts for GP Fusion
We proposed a generalized product of experts (gPoE) framework for combining predictions of multiple Gaussian Process models. The method is highly scalable as individual GP experts can be trained in parallel, while maintaining expressiveness and robustness.
Transductive Log Opinion Pool of GP Experts
Building on the gPoE work, we developed a theoretical framework for analyzing transductive combinations of GP experts. This provides theoretical justification for the empirical success of gPoE while suggesting improvements.
Impact
This series of works has contributed to making Gaussian Process models more practical for large-scale applications by:
- Developing efficient optimization methods with linear complexity
- Creating principled ways to combine multiple GP experts
- Providing theoretical frameworks for understanding model behavior
- Making available open-source implementations
The methods have been applied in various domains requiring probabilistic regression on large datasets.